Researchers at QuTech, a joint venture between TU Delft and TNO, have achieved a quantum error correction milestone.
They've combined high-fidelity operations on encoded quantum data with a scalable data stabilization approach.
The results are published in the December edition of Nature Physics.
Physical quantum bits, also known as qubits, are prone to mistakes. Quantum decoherence, crosstalk, and improper calibration are some of the causes of these problems.
Fortunately, quantum error correction theory suggests that it is possible to compute while simultaneously safeguarding quantum data from such defects.
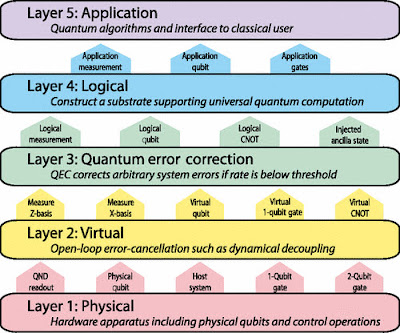
"An error corrected quantum computer will be distinguished from today's noisy intermediate-scale quantum (NISQ) processors by two characteristics," explains QuTech's Prof Leonardo DiCarlo.
- "To begin, it will handle quantum data stored in logical rather than physical qubits (each logical qubit consisting of many physical qubits).
- Second, quantum parity checks will be interspersed with computing stages to discover and fix defects in physical qubits, protecting the encoded information as it is processed."
According to theory, if the occurrence of physical faults is below a threshold and the circuits for logical operations and stabilization are fault resistant, the logical error rate may be exponentially reduced.
The essential principle is that when redundancy is increased and more qubits are used to encode data, the net error decreases.
Researchers from TU Delft and TNO have recently achieved a crucial milestone toward this aim, producing a logical qubit made up of seven physical qubits (superconducting transmons).
"We demonstrate that the encoded data may be used to perform all calculation operations.
A important milestone in quantum error correction is the combination of high-fidelity logical operations with a scalable approach for repetitive stabilization " Prof. Barbara Terhal, also of QuTech, agrees.
Jorge Marques, the first author and Ph.D. candidate, goes on to say,
"Researchers have encoded and stabilized till now. We've now shown that we can also calculate.
This is what a fault-tolerant computer must finally do: handle data while also protecting it from faults.
We do three sorts of logical-qubit operations: initializing it in any state, changing it using gates, and measuring it. We demonstrate that all operations may be performed directly on encoded data.
We find that fault-tolerant versions perform better than non-fault-tolerant variants for each category."
Fault-tolerant processes are essential for preventing physical-qubit faults from becoming logical-qubit errors.
DiCarlo underlines the work's interdisciplinary nature: This is a collaboration between experimental physics, Barbara Terhal's theoretical physics group, and TNO and external colleagues on electronics.
IARPA and Intel Corporation are the primary funders of the project.
"Our ultimate aim is to demonstrate that as we improve encoding redundancy, the net error rate drops exponentially," DiCarlo says.
"Our present concentration is on 17 physical qubits, and we'll move on to 49 in the near future.
Our quantum computer's architecture was built from the ground up to allow for this scalability."
~ Jai Krishna Ponnappan
You may also want to read more about Quantum Computing here.
Further Reading:
J. F. Marques et al, Logical-qubit operations in an error-detecting surface code, Nature Physics (2021). DOI: 10.1038/s41567-021-01423-9