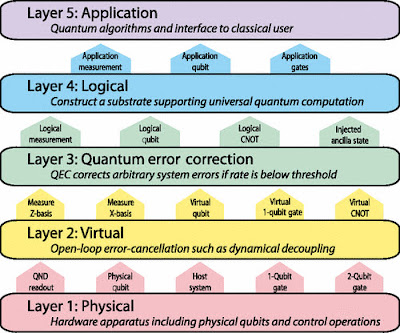
Why is "erasure" essential to creating useful quantum computers?
Researchers have uncovered a brand-new technique for fixing mistakes in quantum computer computations, possibly eliminating a significant roadblock to a powerful new computing domain.
Error correction in traditional computers is a well-established discipline. In order to transmit and receive data across clogged airwaves, every cellphone has to be checked and fixed.
Using very ephemeral subatomic particle characteristics, quantum computers have the incredible potential to tackle certain difficult problems that are intractable for traditional computers.
Even peeking into these computing activities to seek for problems might bring the whole system crashing down since they are so fleeting.
A multidisciplinary team led by Jeff Thompson, an associate professor of electrical and computer engineering at Princeton, and including collaborators Yue Wu, Shruti Puri, and Shimon Kolkowitz from Yale University and the University of Wisconsin-Madison demonstrated how they could significantly increase a quantum computer's tolerance for faults and decrease the amount of redundant information.
The new method doubles the allowed error rate, from 1% to 4%, and makes it workable for developing quantum computers.
The operations you wish to perform on quantum computers are noisy, according to Thompson, which means that computations are subject to a variety of failure scenarios.
An error in a traditional computer may be as basic as a memory bit mistakenly switching from a 1 to a 0, or it can be complex like many wireless routers interfering with one another.
Building in some redundancy to ensure that each piece of data gets examined with duplicate copies is a popular strategy for addressing these problems.
However, such strategy calls for more data and raises the likelihood of mistakes. Therefore, it only functions when the great majority of the available information is accurate.
Otherwise, comparing incorrect data to incorrect data just serves to deepen the inaccuracy.
According to Thompson, redundancy is a terrible technique if your baseline error rate is too high. The biggest obstacle is lowering that barrier.
Thompson's team simply increased the visibility of mistakes rather than concentrating just on lowering the amount of errors.
The researchers studied the physical sources of mistake in great detail and designed their system such that the most frequent source of error effectively destroys the damaged data rather than merely corrupting it.
According to Thompson, this behavior is an example of a specific kind of mistake known as a "erasure error," which is inherently simpler to filter out than damaged data that still seems to be all the other data.
In a traditional computer, it might be dangerous to presume that the slightly more common 1s are accurate and the 0s are incorrect if a packet of presumably duplicate information appears as 11001.
However, the argument is stronger if the information appears as 11XX1, where the damaged bits are obvious.
Because you are aware of the erasure mistakes, Thompson said that they are much simpler to fix. "They could not participate in the majority vote. That is a significant benefit."
Erasure faults in conventional computing are widely recognized, but researchers hadn't previously thought about attempting to construct quantum computers to turn errors into erasures, according to Thompson.
Their device could, in fact, sustain an error rate of 4.1%, which Thompson claimed is well within the range of possibilities for existing quantum computers.
The most advanced error correction in prior systems, according to Thompson, could only tolerate errors of less than 1%, which is beyond the capacity of any existing quantum system with a significant number of qubits.
The team's capacity to produce erasure mistakes ended up being a surprising advantage of a decision Thompson made in the past.
His work examines "neutral atom qubits," in which a single atom is used to store a "qubit" of quantum information.
They were the ones who invented this use of the element ytterbium. As opposed to the majority of other neutral atom qubits, which contain only one electron in their outermost layer of electrons, ytterbium possesses two in this layer, according to Thompson.
As an analogy, Thompson remarked, "I see it as a Swiss army knife, and this ytterbium is the larger, fatter Swiss army knife." "You get a lot of new tools from that additional little bit of complexity you get from having two electrons."
Eliminating mistakes turned out to be one application for those additional tools.
The group suggested boosting ytterbium electrons from their stable "ground state" to excited levels known as "metastable states," which may be long-lived under the appropriate circumstances but are fundamentally brittle.
The researchers' proposal to encode the quantum information using these states is counterintuitive.
The electrons seem to be walking a tightrope, Thompson said. Additionally, the system is designed such that the same elements that lead to inaccuracy also result in electrons slipping off the tightrope.
A collection of ytterbium qubits may be illuminated, but only the defective ones light up because, as an added bonus, the electrons scatter light extremely visibly after they reach the ground state.
Those that illuminate need to be discounted as mistakes.
This development requires merging knowledge from the theory of quantum error correction and the hardware of quantum computing, drawing on the multidisciplinary character of the research team and their close cooperation.
Although the physics of this configuration are unique to Thompson's ytterbium atoms, he said that the notion of building quantum qubits to produce erasure mistakes might be a desirable objective in other systems—of which there are many being developed all over the world—and the group is still working on it.
According to Thompson, other organizations have already started designing their systems to turn mistakes into erasures.
"We view this research as setting out a type of architecture that might be utilized in many various ways," Thompson said. "We already have a lot of interest in discovering adaptations for this task," said the researcher.
Thompson's team is now working on a demonstration of the transformation of mistakes into erasures in a modest operational quantum computer that integrates several tens of qubits as a next step.
The article was published in Nature Communications on August 9 and is titled "Erasure conversion for fault-tolerant quantum computing in alkaline earth Rydberg atom arrays."
Find Jai on Twitter | LinkedIn | Instagram
You may also want to read more about Quantum Computing here.
References And Further Reading:
- Yue Wu et al, Erasure conversion for fault-tolerant quantum computing in alkaline earth Rydberg atom arrays, Nature Communications (2022). DOI: https://dx.doi.org/10.1038/s41467-022-32094-6
- Ponnappan, JK. 2022. Quantum Computing Error Correction - Improving Encoding Redundancy Exponentially Drops Net Error Rate. Technologists In Sync (TS-QC-Jan 22). https://www.technologistsinsync.com/2021/12/quantum-computing-error-correction.html
- Ponnappan, JK. 2022. Fault Tolerance For Quantum Computing Errors. Technologists In Sync (TS-QC-Jan 22). https://www.technologistsinsync.com/2021/10/fault-tolerance-for-quantum-computing.html
- Hilder, J., Pijn, D., Onishchenko, O., Stahl, A., Orth, M., Lekitsch, B., Rodriguez-Blanco, A., Müller, M., Schmidt-Kaler, F. and Poschinger, U.G., 2022. Fault-tolerant parity readout on a shuttling-based trapped-ion quantum computer. Physical Review X, 12(1), p.011032.
- Nakazato, T., Reyes, R., Imaike, N., Matsuda, K., Tsurumoto, K., Sekiguchi, Y. and Kosaka, H., 2022. Quantum error correction of spin quantum memories in diamond under a zero magnetic field. Communications Physics, 5(1), pp.1-7.
- Krinner, S., Lacroix, N., Remm, A., Di Paolo, A., Genois, E., Leroux, C., Hellings, C., Lazar, S., Swiadek, F., Herrmann, J. and Norris, G.J., 2022. Realizing repeated quantum error correction in a distance-three surface code. Nature, 605(7911), pp.669-674.
- Ajagekar, A. and You, F., 2022. New frontiers of quantum computing in chemical engineering. Korean Journal of Chemical Engineering, pp.1-10.