A recent research discloses previously unknown features in Ta2NiSe5, a complicated quantum material.
These results, which were made possible by a new approach pioneered at Penn, have implications for the development of future quantum devices and applications.
This study, which was published in Science Advances, was directed by professor Ritesh Agarwal and done by graduate student Harshvardhan Jog in conjunction with Penn's Eugene Mele and Luminita Harnagea of the Indian Institute of Science Education and Research. (Find Research Paper Attached Below)
While progress has been made in the area of quantum information science in recent years, quantum computers are still in their infancy.
- Because present platforms are not built to enable many qubits to "speak" to one another, one problem is the ability to only employ a minimal number of "qubits," the unit that executes operations in a quantum computer.
- Materials must be efficient at quantum entanglement, which happens when the states of qubits stay connected regardless of their distance from one another, as well as coherence, or when a system can sustain this entanglement, in order to meet this challenge.
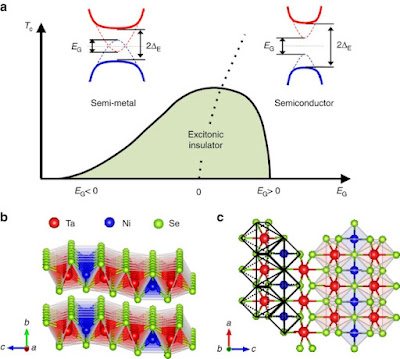
Jog investigated Ta2NiSe5, a material system with high electrical correlation, which makes it suitable for quantum devices.
Strong electronic correlation refers to the relationship between a material's atomic structure and its electronic characteristics, as well as the strong contact between electrons.
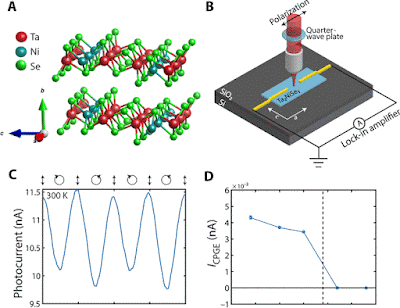
To investigate Ta2NiSe5, Jog modified an Agarwal lab method known as the circular photogalvanic effect, in which light is made to convey an electric field and may be utilized to examine various material characteristics.
This approach, which has been developed and refined over many years, has revealed information about materials such as silicon and Weyl semimetals in ways that are not achievable with traditional physics and materials science research.
But, as Agarwal points out, this method has only been used in materials without inversion symmetry, whereas Ta2NiSe5 does.
Jog "wanted to see if this technique could be used to study materials with inversion symmetry that, from a conventional sense, should not be producing this response," says Agarwal.
Jog and Agarwal employed a modified version of the circular photogalvanic effect after connecting with Harnagea to collect high-quality Ta2NiSe5 samples and were startled to observe that a signal was created.
They collaborated with Mele to build a hypothesis that may help explain these surprising findings after performing more research to assure that this was not a mistake or an experimental artifact.
The difficulty in creating a theory, according to Mele, was that what was anticipated about the symmetry of Ta2NiSe5 did not match the experimental data.
They were then able to offer an explanation for these results after discovering a prior theoretical work that revealed the symmetry was lower than what was expected.
"We recognized that if there was a low-temperature phase when the system spontaneously shears, that would do it," Mele adds.
The researchers discovered that this material had broken symmetry by integrating their experience from both experiment and theory, which was critical to the project's success. This result has major implications for the use of this and other materials in future devices.
This is due to the fact that symmetry is essential for categorizing phases of matter and, eventually, determining their downstream qualities.
These findings may also be used to uncover and describe comparable features in other kinds of materials.
We now have a technology that can detect even the most minute symmetry breaks in crystalline materials.
Symmetries must be considered in order to comprehend any complicated subject since they have enormous ramifications.
While there is still a "far way to go" before Ta2NiSe5 can be used in quantum devices, the researchers are already working to better understand this phenomena.
In the lab, Jog and Agarwal are interested in searching for possible topological qualities in extra energy levels inside Ta2NiSe5, as well as utilizing the circular photogalvanic approach to look at other associated systems to see if they have comparable properties.
Mele is investigating how often this phenomenon is in various material systems and generating recommendations for new materials for experimentalists to investigate.
"What we're seeing here is a reaction that shouldn't happen but does in this situation," Mele adds.
"Expanding the area of structures available to you, where you may activate these effects that are ostensibly disallowed, is critical. It's not the first time something has occurred in spectroscopy, but it's always intriguing when it occurs."
This work not only introduces the research community to a new tool for studying complex crystals, but it also sheds light on the types of materials that can provide two key features, entanglement and macroscopic coherence, which are critical for future quantum applications ranging from medical diagnostics to low-power electronics and sensors.
"The long-term aim, and one of the most important goals in condensed matter physics," adds Agarwal, "is to be able to comprehend these highly entangled states of matter because these materials can conduct a lot of intricate modeling." "
It's possible that if we can figure out how to comprehend these systems, they'll become natural platforms for large-scale quantum simulation."
References:
Harshvardhan Jog et al, Exchange coupling–mediated broken symmetries in Ta 2 NiSe 5 revealed from quadrupolar circular photogalvanic effect, Science Advances (2022). DOI: 10.1126/sciadv.abl9020
Jog, H., Harnagea, L., Mele, E. and Agarwal, R., 2021. Circular photogalvanic effect in inversion symmetric crystal: the case of ferro-rotational order in Ta 2 NiSe 5. Bulletin of the American Physical Society, 66.
You may also want to read more about Quantum Computing here.