"Machine learning," a phrase originated by Arthur Samuel in 1959, is a kind of artificial intelligence that produces results without requiring explicit programming.
Instead, the system learns from a database on its own and improves over time.
Machine learning techniques have a wide range of applications (e.g., computer vision, natural language processing, autonomous gaming agents, classification, and regressions) and are used in practically every sector due to their resilience and simplicity of implementation (e.g., tech, finance, research, education, gaming, and navigation).
Machine learning algorithms may be generically classified into three learning types: supervised, unsupervised, and reinforcement, notwithstanding their vast range of applications.
Supervised learning is exemplified by machine learning regressions.
They use algorithms that have been trained on data with labeled continuous numerical outputs.
The quantity of training data or validation criteria required once the regression algorithm has been suitably trained and verified will depend on the issues being addressed.
For data with comparable input structures, the newly developed predictive models give inferred outputs.
These aren't static models.
They may be updated on a regular basis with new training data or by displaying the actual right outputs on previously unlabeled inputs.
Despite machine learning methods' generalizability, there is no one program that is optimal for all regression issues.
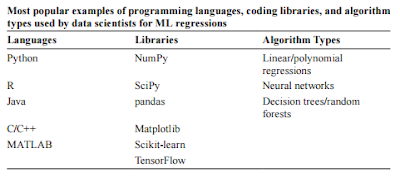
When choosing the best machine learning regression method for the present situation, there are a lot of things to think about (e.g., programming languages, available libraries, algorithm types, data size, and data structure).
There are machine learning programs that employ single or multivariable linear regression approaches, much like other classic statistical methods.
These models represent the connections between a single or several independent feature variables and a dependent target variable.
The models provide linear representations of the combined input variables as their output.
These models are only applicable to noncomplex and small data sets.
Polynomial regressions may be used with nonlinear data.
This necessitates the programmers' knowledge of the data structure, which is often the goal of utilizing machine learning models in the first place.
These methods are unlikely to be appropriate for most real-world data, but they give a basic starting point and might provide users with models that are straightforward to understand.
Decision trees, as the name implies, are tree-like structures that map the input features/attributes of programs to determine the eventual output goal.
The answer to the condition of that node splits into edges in a decision tree algorithm, which starts with the root node (i.e., an input variable).
A leaf is defined as an edge that no longer divides; an internal edge is defined as one that continues to split.
For example, age, weight, and family diabetic history might be used as input factors in a dataset of diabetic and nondiabetic patients to estimate the likelihood of a new patient developing diabetes.
The age variable might be used as the root node (e.g., age 40), with the dataset being divided into those who are more than or equal to 40 and those who are 39 and younger.
The model provides that leaf as the final output if the following internal node after picking more than or equal to 40 is whether or not a parent has/had diabetes, and the leaf estimates the affirmative responses to have a 60% likelihood of this patient acquiring diabetes.
This is a very basic decision tree that demonstrates the decision-making process.
Thousands of nodes may readily be found in a decision tree.
Random forest algorithms are just decision tree mashups.
They are made up of hundreds of decision trees, the ultimate outputs of which are the averaged outputs of the individual trees.
Although decision trees and random forests are excellent at learning very complex data structures, they are prone to overfitting.
With adequate pruning (e.g., establishing the n values limits for splitting and leaves) and big enough random forests, overfitting may be reduced.
Machine learning techniques inspired by the neural connections of the human brain are known as neural networks.
Neurons are the basic unit of neural network algorithms, much as they are in the human brain, and they are organized into numerous layers.
The input layer contains the input variables, the hidden layers include the layers of neurons (there may be numerous hidden levels), and the output layer contains the final neuron.
A single neuron in a feedforward process
(a) takes the input feature variables,
(b) multiplies the feature values by a weight,
(c) adds the resultant feature products, together with a bias variable, and
(d) passes the sums through an activation function, most often a sigmoid function.
The partial derivative computations of the previous neurons and neural layers are used to alter the weights and biases of each neuron.
Backpropagation is the term for this practice.
The output of the activation function of a single neuron is distributed to all neurons in the next hidden layer or final output layer.
As a result, the projected value is the last neuron's output.
Because neural networks are exceptionally adept at learning exceedingly complicated variable associations, programmers may spend less time reconstructing their data.
Neural network models, on the other hand, are difficult to interpret due to their complexity, and the intervariable relationships are largely hidden.
When used on extremely big datasets, neural networks operate best.
They need meticulous hyper-tuning and considerable processing capacity.
For data scientists attempting to comprehend massive datasets, machine learning has become the standard technique.
Machine learning systems are always being improved in terms of accuracy and usability by researchers.
Machine learning algorithms, on the other hand, are only as useful as the data used to train the model.
Poor data produces dramatically erroneous outcomes, while biased data combined with a lack of knowledge deepens societal disparities.
You may also want to read more about Artificial Intelligence here.
See also:
Algorithmic Bias and Error; Automated Machine Learning; Deep Learning; Explainable AI; Gender and AI.
Further Reading:
Garcia, Megan. 2016. “Racist in the Machine: The Disturbing Implications of Algorithmic Bias.” World Policy Journal 33, no. 4 (Winter): 111–17.
Géron, Aurelien. 2019. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. Sebastopol, CA: O’Reilly.