What Is The ARTMAP-IC Algorithm?
The fundamental fuzzy ARTMAP is enhanced by this network with distributed prediction and category instance counting.
How Is The ARTMAP-IC Used For Medical Diagnosis?
Medical diagnosis with ARTMAP-IC: Inconsistent cases and instance counting.
The ARTMAP-IC neural network extends the fundamental fuzzy ARTMAP system with distributed prediction and category instance counting for challenging database prediction issues like medical diagnosis.
A new version of the ARTMAP match tracking algorithm, which governs search after a predictive mistake, makes prediction with sparse or inconsistent data easier.
The new approach (MT-) significantly compresses memory without sacrificing speed while improving the accuracy of the real-time network differential equations as compared to the old match tracking algorithm (MT+).
Simulated analyses of four medical databases—Pima Indian diabetes, breast cancer, heart disease, and gallbladder removal—examine the prognostic accuracy of these conditions.
Results using logistic regression, K closest neighbor (KNN), the ADAP preceptron, multisurface pattern separation, CLASSIT, instance-based (IBL), and C4 are comparable to or superior to those from ARTMAP-IC.
The dynamics of ARTMAP are quick, reliable, and scalable.
By repeatedly training the system on various input set orderings, a voting technique enhances prediction.
Confidence intervals for competing predictions are derived from voting, instance counting, and distributed representations.
HOW DOES ARTMAP-IC NEURAL NETWORK CLASSIFIER FUNCTION?
In an ART-based network, information reverberates between the network’s layers.
Learning is possible in the network, when resonance of the neuronal activity occurs. ART1 was developed to perform clustering on binary-valued patterns.
By interconnecting two ART1 modules, ARTMAP was the first ART-based architecture suited for classification tasks.
ARTMAP- IC adds to the basic ARTMAP system new capabilities designed to solve the problem with inconsistent cases, which arises in prediction, where similar input vectors correspond to cases with different outcomes, (Carpenter, Grossberg, and Reynolds, 1991), (Carpenter and Markuzon, 1998).
It modifies the ARTMAP search algorithm to allow the network to encode inconsistent cases (IC).
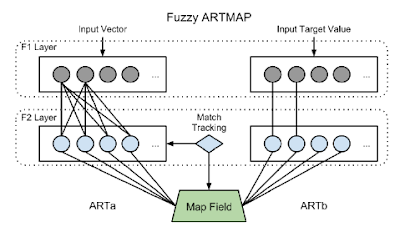
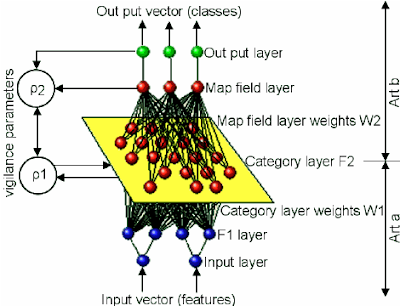
Below figure, adapted from (Carpenter and Markuzon, 1998), shows the architecture of an ARTMAP-IC network.
It consist of fully connected layers of nodes: an M-node input layer F1, an Nnode competitive layer F2, an N-node instance counting layer F3, an L-node output layer F0 b , and an L-node map field Fab that links F3 and F0 b .
In ARTMAP-IC an input a=(a1, a2, … , aM) learns to predict an outcome b=(b1, b2, …, bL), , where only one component bK=1, placing the input a in class K.
With fast learning, β=1, ARTMAP-IC represents category K as hyper-rectangle ℜK that just encloses all the training set patterns a to which it has been assigned.
A set of real weights W={wji: j=1,…,N; i=1,…,M} is associated with the F1 - F2 layer connections. Each F2 node j represents a category in the input space, and stores a prototype vector wj=(wj1, wj2, …,wjM).
The F2 layer is connected, through associative links to F3, which in turn is connected to the map field Fab by associative links with binary weights Wab=(wjk ab:j=1,…,N; k=1,…,L}.
The vector wj ab=(wj1 ab, wj2 ab, …,wjL ab) relates F2 node j to one of the L output classes. Instance counting biases distributed predictions according to the number of training set inputs classified by each F2 node.
During testing the F2->F3 input yj is multiplied by the counting weight cj to produce normalized F3 activity, which projects to the map field Fab for prediction.
How Does The ARTMAP-IC Algorithm Operate In Classifier Mode?
The following algorithm describes the operation of an ARTMAP-IC classifier in learning mode:
1. Initialization:
Initially, all the neurons of F2 are uncommitted, all weight values wji are initialized to 1, and all weight values wjk of Fab are set to 0.
2. Input pattern coding:
When a training pair (a,b) is presented to the network, a undergoes preprocessing, and yields pattern A=(A1,A2,…,A2M).
The vigilance parameter ρ is reset to its baseline value.
3. Prototype selection:
Pattern A activates layer F1 and is propagated through weighted connections W to layer F2.
Activation of each node j in the F2 layer is determined by the choice function Tj(A)=|A∧wj|/(α+|wj|).
The F2 layer produces a winner-take-all pattern of activity y=(y1,y2,…,yN) such that only node j=J with the greatest activation value remains active (yJ=1).
Node J propagates its prototype vector wJ back onto F1 and the vigilance test |A∧wj|≥ρM is performed.
This test compares the degree of match between wJ and A to the vigilance parameter ρ∈[0,1].
If this test is satisfied, node J remains active and resonance is said to occur.
Otherwise, the network inhibits the active F2 node and searches for another node J that passes the vigilance test.
If such a node does not exist, an uncommitted F2 node becomes active and undergoes learning (step 5).
4. Class prediction:
Pattern b is fed directly to the map field Fab, while the F2 activity pattern y is propagated to the map field via associative connections Wab.
The latter input activates Fab nodes according to the prediction function ∑= = N j ab j jk ab Sk y y w 1 ( ) and the most active Fab node K yields the class prediction (K=k(J)).
If node K constitutes an incorrect class prediction, a match tracking signal raises vigilance just enough to induce another search among F2 nodes (step 3).
This search continues until either an uncommitted F2 node becomes active (learning ensues at step 5), or a node J that has previously learned the correct class prediction K becomes active.
5. Learning:
Learning input a involves updating prototype vector wJ, and if J corresponds to a newly committed node, creating a permanent associative link to Fab.
A new association between F2 node J and Fab node K (K=k(J)) is learned by setting wJk ab=1 for k=K, where K is the target class label for a.
Once the weights (W and Wab) have converged for the training set patterns, ARTMAP can predict a class label for an input pattern by performing steps 2, 3 and 4 without any testing.
A pattern a that activates node J is predicted to belong to the class K=k(J)
Find Jai on Twitter | LinkedIn | Instagram
Be sure to refer to the complete & active AI Terms Glossary here.
You may also want to read more about Artificial Intelligence here.
Reference And Further Reading
- Tayyebi, S. and Soltanali, S., Fuzzy Modeling System Based on Ga Fuzzy Rule Extraction and Hybrid of Differential Evolution and Tabu Search Approaches: Application in Synthesis Gas Conversion to Valuable Hydrocarbons Process. Saeed, Fuzzy Modeling System Based on Ga Fuzzy Rule Extraction and Hybrid of Differential Evolution and Tabu Search Approaches: Application in Synthesis Gas Conversion to Valuable Hydrocarbons Process.
- Tang, Y., Qiu, J. and Gao, M., 2022. Fuzzy Medical Computer Vision Image Restoration and Visual Application. Computational and Mathematical Methods in Medicine, 2022.
- Dymora, P., Mazurek, M. and Bomba, S., 2022. A Comparative Analysis of Selected Predictive Algorithms in Control of Machine Processes. Energies 2022, 15, 1895.
- Naosekpam, V. and Sahu, N., 2022, April. IFVSNet: Intermediate Features Fusion based CNN for Video Subtitles Identification. In 2022 IEEE 7th International conference for Convergence in Technology (I2CT) (pp. 1-6). IEEE.
- Boga, J. and Kumar, V.D., 2022. Human activity recognition by wireless body area networks through multi‐objective feature selection with deep learning. Expert Systems, p.e12988.
- Župerl, U., Stepien, K., Munđar, G. and Kovačič, M., 2022. A Cloud-Based System for the Optical Monitoring of Tool Conditions during Milling through the Detection of Chip Surface Size and Identification of Cutting Force Trends. Processes, 10(4), p.671.
- Neto, J.B.C., Ferrari, C., Marana, A.N., Berretti, S. and Bimbo, A.D., 2022. Learning Streamed Attention Network from Descriptor Images for Cross-resolution 3D Face Recognition. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM).
- Chattopadhyay, S., Dey, A., Singh, P.K., Ahmadian, A. and Sarkar, R., 2022. A feature selection model for speech emotion recognition using clustering-based population generation with hybrid of equilibrium optimizer and atom search optimization algorithm. Multimedia Tools and Applications, pp.1-34.
- Kanagaraj, R., Elakiya, E., Rajkumar, N., Srinivasan, K. and Sriram, S., 2022, January. Fuzzy Neural Network Classification Model for Multi Labeled Electricity Consumption Data Set. In 2022 4th International Conference on Smart Systems and Inventive Technology (ICSSIT) (pp. 1037-1041). IEEE.